Knowledge is POWER
علمیKnowledge is POWER
علمیابر مکعب!
همه میدونیم که نقطه بدونه بعد خط یک بعدی و مربع دو بعدیست...
آیا شکل ۴بعدی هم تابحال دیدید؟
راجع به بعد چهارم تو ریاضیات چی میدونید؟
در هندسه، یک اَبَرمکعب، یک چند-بعدی پیوسته از یک مربع (۲=n) و یک مکعب (۳=n)است. فوق مکعب، یک شکل محدب فشرده بسته، است که از یک ساختار متشکل از گروه پارهخطهای موازی متقابل، در هریک از ابعاد فضا، با زاویههای عمود بر یکدیگر و طول یکسان تشکیل شدهاست.
یک اَبَرمکعب چند بُعدی با نام چندمکعب (n-cube) نیز نامیده میشود. از اصطلاح«measure polytope» نیز معمولا استفاده میشود، به طور مشخص در عمل، هارولد اسکات مکدونالد کوکسِتر (H.S.M. Coxeter)از این اصطلاح استفاده کردهاست که اکنون این واژه کنار گذاشته میشود. یک ابرمکعب حالت خاصی از اَبَر مکعبمستطیل است، که با نام ارتوتوپ(orthotope) نیز نامیده میشود. یک ابرمکعب یکه (واحد)، یک فوقمکعب با طول ضلع 1 است. اغلب در فضای nبعدی Rn، گوشهها یا رأسهای فوقمکعب واحد تعداد 2n نقطه، با مختصات ۰ یا ۱ است.
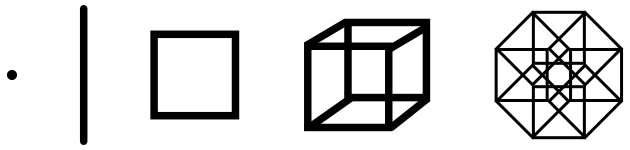
نقطه به عنوان ابرمکعب
یک نقطه، یک اَبَرمکعب با بعد صفر است. یعنی نقطه را میتوان نوعی فوقمکعب در فضای R0 نامید. اگر این نقطه به اندازهی یک واحد به سمتی، حرکت کند، یک پارهخط پدید میآورد. یا به اصطلاح، مسیری را که طی میکند یک پارهخط است. پارهخط یک اَبرمکعب با بعد یک است. به بیان دیگر، پارهخط نوعی فوقمکعب در فضای R1 است.
اگر این پارهخط در امتدادی عمود بر طول خودش، به اندازه یک واحد جابجا شود، سطحی دوبعدی به شکل مربع پدید میآورد. این مربع، یک ابرمکعب در فضای R2 خواهد بود. به همین ترتیب، اگر مربع را به اندازهی یک واحد، در راستای عمود بر سطح خودش، جابجا کنیم، یک مکعب سهبعدی پدید خواهد آمد (ابرمکعبی در فضای ریاضی R3). این شیوه در باره فضای چندبعدی، و دستیابی به ابرمکعبهای nبعدی نیز قابل گسترش است. برای مثال، اگر یک مکعب 3بعدی را در راستای بُعد چهارمش به اندازهی یک واحد، جابجا کنیم، یک ابرمکعب 4بعدی با ابعاد واحد بهدست خواهد آمد.
این فرآیند حرکت بر امتداد عمود بر شیء، میتواند به شیوهی ریاضی با جمع مینکوفسکی بیان شود.
ابرمکعب dبعدی، یک جمع مینکوفسکی از پارهخطهای دوبدو متعامد شکل گرفته و در نتیجه یک مثال از زونوتوپ است.
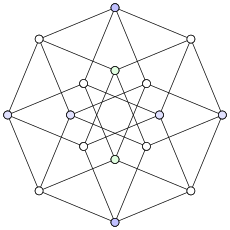
از دیدگاه ریختشناسی (توپولوژی) ساختار تک-اسکلتی ابرمکعب یک گراف ابرمکعب است.
مختصات
یک ابرمکعب یکهی چندبعدی، یک سطح محدب از نقاط با دگرگونىهاى علامت در مختصات کارتزین است 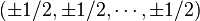 . طول هر ضلع آن برابر 1 و حجمش نیز 1 واحد است.
. طول هر ضلع آن برابر 1 و حجمش نیز 1 واحد است.
همچنین یک ابرمکعب n-بعدى اغلب به عنوان رویهی محدب تلقی شدهاست 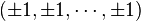 . اغلب این فرم بهخاطر سهولت در نوشتن مختصات انتخاب شدهاست. طول لبهى آن 2 است و رتبه n-بعدیاش نیز 2 است (n2).
. اغلب این فرم بهخاطر سهولت در نوشتن مختصات انتخاب شدهاست. طول لبهى آن 2 است و رتبه n-بعدیاش نیز 2 است (n2).
تسرکت
در هندسه، به همتای چهاربعدی یک مکعب (سهبُعدی) تِسِرَکت میگویند.
حرکت در راستای بعد چهارم یک تسرکت، نماینده تغییر شکل کرانمند مکعب در جریان زمان است.
طریقه ترسیم یک تسرکت
- پله اول : ترسیم یک مربع به روی دستگاه مختصات دکارتی
- پله دوم : ترسیم نسخه عینی از همان مربع در پائین مربع قبلی (در جهت محور z)
- پله سوم : تشکیل یک مکعب با کشیدن ٤ خط اریب
- پله چهارم : ترسیم خطوط مورب از هر ٨ گوشهٔ مکعب قبلی در جهت محور w. انتهای هیچ یک از این خطوط نباید در گوشههای قبلی قرار گیرد.
- پله پنجم : اضافه کردن ٤ خط افقی, ٤ خط عمودی و ٤ خط "z"







هزاران درود بر شما
فرق العاده بود.و خیلی استفاده کردم.
ممنون
tnx. aaalii boood, estefade kardam.
عالی بودددد...من همیشه مطالب مربوط به فیزیک فرابعدی رو دوست داشتم و دارم.هرچیزی که مربوط به فضا میشه.مرسی
wowwwwwwww چ باحال